Recall the Stefan-Boltzmann formula:
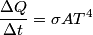 Here 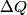 / /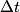 is the rate at which energy is radiated from the blackbody, is the rate at which energy is radiated from the blackbody, 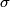 is the Stefan-Boltzmann constant, is the Stefan-Boltzmann constant, 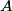 is the area of the blackbody, and is the area of the blackbody, and 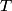 is the temperature of the blackbody in is the temperature of the blackbody in 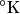 . So, doubling . So, doubling 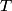 increases the power radiated by the blackbody by a factor of increases the power radiated by the blackbody by a factor of 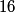 . Assuming the heat capacity of the water is constant over the relevant temperature range, this means that the temperature would increase . Assuming the heat capacity of the water is constant over the relevant temperature range, this means that the temperature would increase 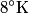 instead of instead of 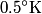 . Therefore, answer (C) is correct. . Therefore, answer (C) is correct. |